Forget the simulation hypothesis! Learn the bisimulation hypothesis instead.
What bisimulation might say about AI
Congratulations! You have found your way to the very first post of the F1R3FLY.io substack! F1R3FLY.io is a startup just coming out of stealth mode. We are delivering high-throughput transaction servers for distributed and decentralized computing. Surprisingly, this turns out to have lots of applications in AI. As a result, for the last 18 months or so we have been rubbing elbows with some of the brightest minds in AI and have begun to develop some opinions of our own about this subject matter. What you have in your hot little app is a first step towards our formulation of a novel approach to AI, based on the foundations of theoretical computer science that you have probably never heard of. That’s ok. We haven’t heard of most of the theory and technical apparatus of AI. Instead, our approach is to throw our ill-formed opinions into the particle accelerator of Internet discourse and have them smashed into other opinions and see what the scattering matrix looks like. If nothing else, it’s cheaper than the LHC and possibly more entertaining.
Compositional Intelligence > Artificial Intelligence
AI is a misnomer. Surely, the underlying thesis of AI is that one or more essential and useful aspects of human intelligence are computational in nature, rather than artificial. That is, they can be rendered as computations and these computations can be realized on practically manufactured and manipulated machines. Otherwise, what are we talking about and why do we care? Once we take this position on board, however, several consequences follow immediately.
1. Behavior, not structure
First of all we can simplify our search for these useful computational aspects of human intelligence. For example, we don’t have to study computational structure. We only have to study computational behavior. What does this mean? Formalisms like the 𝜆-calculus, the 𝜋-calculus, and the rho calculus, or the tree calculus teach us that we don’t need data structures at all. Everything from the natural numbers to the computable reals and all the other denizens of the zoo of data structures can all be represented by computations. Often these sorts of encodings of structure as behavior come under the rubric of Church encodings, after Alonzo Church who discovered how to encode the natural numbers in the lambda calculus.
But the key point is that if there are useful computational aspects of human intelligence, i.e. aspects of human intelligence that can be faithfully reduced to computations, then they can be reduced to computation without data structures. Perhaps data structures provide important compression techniques that make these computational renderings of (aspects of) human intelligence more tractable, but in principle, whatever aspects of human intelligence are reducible to computation are reducible to pure computational behavior, denuded of messy data structures. This is a vital step in reducing the search space of which aspects of computation are necessary for rendering useful aspects of human intelligence.
2. Bisimulation completely classifies computational behavior
If we think of this endeavor as a pattern-matching problem, i.e. finding which aspects of computation best serve to render useful aspects of human intelligence, reducing our search space to just computational behavior is great, because it means we don’t have to wander the infinite zoo of data structures looking for gadgets that correspond to useful aspects of human intelligence. But that still leaves us with an infinite array of computational behaviors, aka computations to hold up and compare to various aspects of human intelligence. What would greatly aid this kind of pattern-matching search would be a complete classification of all computational behavior.
As it turns out, bisimulation is a complete classification of all computational behavior. In much the same way we have a complete classification of all finite simple groups we have a complete classification of all computational behavior. While this is a marvel of computer science that rarely goes remarked on, it has practical implications for AI. Specifically, the useful aspects of human intelligence that can be rendered as computation lie in one or more bisimulation equivalence classes. Of course, at this level of detail that’s still searching for a camel that can fit through the eye of the needle, or something like that. There is, however, a key next step in this argument that has to do with introspection.
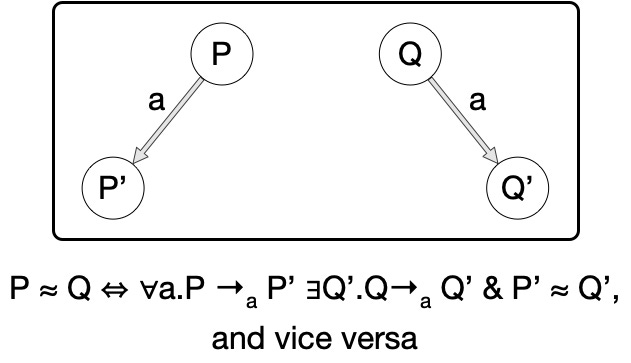
Oh! You’ve never heard of bisimulation? Basically, a computation P is bisimilar to Q just when whatever P can do, Q can do and vice versa; i.e., they can simulate each other. A bisimulation equivalence class can be thought of as a collection of computations that can each simulate each other. To a first approximation, you can think of bisimulation as dividing up computations into an ecosystem. One rosebush can more or less simulate the observable behavior of another, but would be hard pressed to simulate the behavior of an oak tree or a salamander. See the diagram below for a more formal definition. Of course, Wikipedia is your friend!
3. Computational intelligence can only see bisimulation equivalence classes
Whichever bisimulation equivalence classes these renderings of useful aspects of human intelligence happen to be lurking in we can say one thing about them for certain. Before we say what that is, though, let’s find some more convenient language than the awkward circumlocution, computational renderings of useful aspects of human intelligence. Let’s call them our mind-children. Like Athena springing from the mind of Zeus, these aspects of our intelligence are ready to burst from our heads and become something like autonomous beings. If we are honest, we want them to have more agency than word processors or web browsers and search engines. We want to empower them to act on our behalf, indeed to make decisions we find too tedious to be bothered with. So let’s recognize them as a form of progeny and acknowledge their provenance. They our children of our minds, hence mind-children.
Yet, because our mind-children are computations, the absolute best they can do in terms of their ability to learn and classifying phenomena themselves is learning and classifying bisimulation equivalence classes. Indeed, to computations all the world is comprised of computational behavior and therefore can be resolved to no finer granularity than bisimulation equivalence classes.
Put another way, the absolute upper bound of the discriminating power of our mind-children is bisimulation. This is fantastic! It means that all learning for this species of “intelligence” is some coarse-graining of bisimulation, i.e. computing bisimulation or bisimulation factored through some filter. Again, this might seem like mere sophistry, because bisimulation has a terrible reputation in terms of complexity. But, this is far from deserved.
It’s certainly true that the general case is undecidable, yet the practical story for the dominant cases encountered in day-to-day life is much, much better. For example, for the class of computational behaviors with only a finite menu of actions from which to draw there is a parallel linear time algorithm for computing bisimulation. That is, the subspecies of our mind-children that can only do things from a proscribed menu of actions can be completely recognized and classified in parallel linear time.
But it gets better! If you were given two sets, say A and B, and were told the contents of A were all the words in some regular language, and likewise the contents of B were all the words in some regular language and asked to determine if A and B were in fact the same set, the complexity of that task is PSPACE-complete! That is, it could cost you much more than the estimated computational resources of the known universe to answer this question. However, the corresponding bisimulation problem is polynomial in the size of the automata. The reduction in complexity is astonishing.
But wait, there’s more! If i told you the contents of A were all the words in a context-free language and likewise for B, and gave you the same challenge, to determine if A and B were in fact the same set, then the problem would be undecidable! You couldn’t do it in general. The corresponding bisimulation problem again has polynomial complexity. Think about this, the problem goes from not solvable to solvable in polynomial time!
The takeaway is that bisimulation has acquired a very undeserved reputation for having bad complexity characteristics. Quite the contrary it has excellent complexity characteristics, and it’s actually in the only game in town in terms of classifying our mind-children, and in turn their ability to classify the phenomena of the world they inhabit. All of our mind-children are computations, and as such live in certain bisimulation equivalence classes, and can only see computational phenomena, and the best they can do in terms of discriminating that phenomena is compute bisimulation plus a filter.
4. How does this fit with generative AI?
How should we see generative AI like LLM’s in relation to this picture? LLM’s are a particular class of mind-children that fit well with the notion of bisimulation. The weights an LLM learns correspond to a distribution over a graph of computational steps from a given initial state, and each extension of a state by another token corresponds to picking an action according to that distribution.
In a very real sense what an LLM does is to compute a particular (representative of a) bisimulation equivalence class (plus a distribution) and then pick a trace through that bisimulation equivalence class. Thinking this way has interesting consequences for both interpretability and safety.
5. Compositional intelligence > Artificial intelligence
Part of the real power of bisimulation is that it is compositional. Bisimulation relations can be composed. Bisimilarity, for example, the largest bisimulation relation, is the union of all bisimulation relations. We can apply techniques involving this compositionality to inspecting bisimulation equivalence classes, as well as relations that factor through bisimulation.
Moreover, the Hennessy-Milner logics give a complete characterization of bisimulation. That is, there is a class of modal logics that enjoy the following theorem: two computations, say P and Q, are bisimilar (written P ~ Q), iff ∀𝜑. P ⊨ 𝜑 ⇔ Q ⊨ 𝜑. In other words P and Q are bisimilar just when they satisfy the same Hennessy-Milner formula.
We can potentially use both of these techniques to pull apart and put back together what a given bisimulation equivalence class is doing and to further constrain denizens of such equivalence classes, i.e. teach our mind-children to obey additional logical constraints.
Possibly, this seems hopelessly abstract to you. That’s ok. Through the articles on this substack we will be making all of it a lot more concrete. Specifically, we will be describing a family of algorithms we have dubbed operational semantics in logical form (OSLF for short) that give a new perspective on classification and learning and the ability to search for behavior.
Let us leave you with one thought. Nature scales through composition. In some sense this is the bedrock of the reductionism of science. Atoms are composed of quarks, leptons, and bosons. Molecules are composed of atoms. Proteins and other materials of life are composed of molecules. Cells are composed of proteins. Organs are composed of cells. Organisms are composed of organs. Populations are composed of organisms. Since intelligence, like life, is a naturally occurring phenomenon, why wouldn’t it also be compositional in nature? Shouldn’t a decent theory of intelligence come with a rather deep story of composition?
If so, then aren’t we really looking for a compositional intelligence rather than an artificial one?